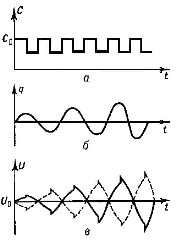
Параметрический резонанс – явление раскачки колебаний при периодическом изменении параметров тех элементов колебательной системы, в которых сосредоточивается энергия колебаний (реактивные или энергоемкие параметры). Параметрический резонанс возможен в колебательных системах различной природы. Например в электрическом колебательном контуре реактивными параметрами являются ёмкость С и индуктивность L, в которых запасены электрическая энергия Wэ=q2/2С и магнитной энергии Wм=LI2/2 (где q – заряд на обкладках конденсатора, I – ток в катушке индуктивности). Собственные колебания в контуре без потерь с постоянными C и L происходят с частотой ωо2 = 1/LC. При этом полная энергия W = Wэ +Wм, запасенная в контуре, остается неизменной, происходит лишь ее периодическая трансформация из электрической в магнитную и обратно с частотой 2ωо. Изменение параметров C и L сопровождается работой внешних сил (накачка), приводит к изменению полной энергии системы. Если емкость C изменить скачком за время, малое по сравнению с периодом собственных колебаний T0=2π2/ω0 (рис.1а), то заряд скачком измениться не может (поскольку сила тока остается конечной величиной, рис.1б). В результате напряжение на емкости U=q/c (рис.1в) и электрическая энергия Wэ изменяются обратно пропорционально C, причем совершаемая при этом работа пропорциональна q2. Если изменять емкость C периодически в такт изменениям Wэ (обусловленным собственными колебаниями), уменьшая ее в моменты когда q2 и Wэ максимальны, и увеличивая, когда эти величины равны нулю (рис.1) то в среднем за период над системой совершается положительная работа и, следовательно, полная энергия и амплитуда будут монотонно нарастать.
Связь между изменениями емкости C конденсатора (а), заряда q на его обкладках (б) и напряжения U (в) при параметрическом резонансе в колебательном контуре.
Рис.1
Параметрический резонанс наиболее эффективно проявляется при изменении параметров колебательной системы с периодом Tн, кратным полупериоду собственных колебаний T0:
Tн ≈ nT0/2, ωн=2ω0/n (1)
где n – целое число, ωн=2π/Tн – частота накачки. Математически свободные колебания в таких системах описываются дифференциальными уравнениями с переменными коэффициентами. Например, в случае колебательного контура с переменной емкостью C(t) (в отсутствии омического сопротивления) уравнение относительного заряда q(t) имеет вид:
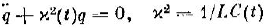
(2)
(уравнение Хилла). согласно теореме Флоке общее решение (2) можно записать в виде:
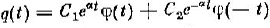
(3)
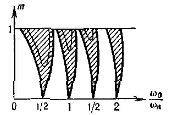
Где C1,2 – произвольные коэффициенты, определяемые начальными условиями, φ(t) – периодичность функции с периодом Tн, α - коэффициент, зависящий от параметров системы. При выполнении условия (1) Reα ≠ 0 и один из членов (3) дает нарастающие во времени колебания. Наиболее быстрая раскачка имеет место при n=1, когда частота накачки ωн равна частоте колебаний величин Wэ и Wм в системе (2ω0). Нарастание колебаний возможно не только при точном выполнении соотношений (1), но и в некоторых конечных интервалах значений ωн вблизи 2ω0/n (в зонах неустойчивости), ширина зон тем больше, чем сильнее изменяются параметры C и L. Изменение параметра, например емкости C, характеризуют величиной
m = (Cмакс – Cмин)/(Cмин + Cмин),
называется
глубиной параметра. В частном случае синусоидального изменения
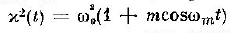
[уравнение (2) при этом называется уравнением Матье] в основной зоне (n=1) при
m << 1 инкремент
α равен
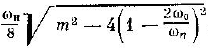
,
так что в середине зоны α = mω0/4; во второй зоне (n=2) α ~ m2, в третьей α ~ m3, и так далее.
Существенная особенность параметрического резонанса в системах с распределёнными параметрами состоит в том, что его эффективность зависит от соотношения между законом изменения параметров системы в пространстве и пространственной структурой колебаний (волн). Например, если накачка, изменяющая параметры среды, представляет собой бегущую волну с частотой ωн и волновым вектором kн, то возбуждение пары нормальных волн с частотами ω1, ω2 и волновыми векторами k1, k2 осуществляется, если выполняются условия параметрического резонанса как во времени, так и в пространстве:
ωн=ω1 + ω2; kн=k1 + k2 (4)
На квантовом языке эти условия означают, что при распаде кванта накачки сохраняются как энергия, так и импульс (ћk). Нарастание амплитуд волн во времени и пространстве (распадная неустойчивость) также ограничивается нелинейными эффектами: если значительная часть энергии накачки израсходована на возбуждение этих волн, то возможен обратный процесс — рост энергии накачки за счет ослабления волн на частотах ω1, ω2; в среде без потерь такой обмен энергией происходит периодически.
Параметрический резонанс от силового резонанса отличается формой резонансной кривой - вслучае параметрического возбуждения колебаний резонанс наблюдается в строго ограниченой полосе частот (которая определяется значением n и амплитудой изменения параметра), в то время как при силовом воздействии на систему можно добиться существования колебаний на любой частоте.
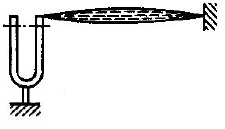
В колебательных системах с распределенными параметрами, обладающих бесконечным числом степеней свободы, возможно возбуждение нормальных колебаний в результате параметрического резонанса. Классический пример — опыт Мельде (1859), в котором наблюдалось возбуждение поперечных колебаний (стоячих волн) в струне, прикрепленной одним концом к ножке камертона, колебания которого периодически меняют натяжение струны (рис. 1) с частотой, вдвое большей частоты собственных поперечных колебаний. Легче всего параметрический резонанс возникает, когда один из периодов собственных колебаний струны (её основного тона или какого-либо из гармоник) приблизительно вдвое больше периода колебаний камертона. При обычном же возбуждении вынужденных колебаний струны с периодом, равным периоду колебаний камертона, резонанс наступил бы всякий раз, когда период колебаний камертона совпадал бы с периодом одного из собственных колебаний струны. Таким образом, явление параметрического резонанса в этом отношении сходно с силовым резонансом при возбуждении вынужденных колебаний.
Параметрический резонанс может приводить к раскачке изгибных колебаний вращающихся валов.
Другой пример — опыт Фарадея (1831), в котором вертикальные колебания сосуда с водой приводят к возбуждению стоячей поверхностной волны с удвоенным периодом.
Параметрические и нелинейные резонансные взаимодействия волн характерны для различных типов волн в плазме, мощных световых волн, волн в электронных пучках и др. волновых процессов.
Параметрическое возбуждение колебаний струны
Рис.2
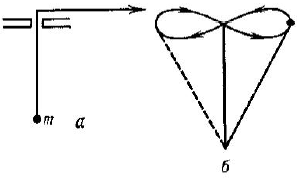
Пример механической системы, в которой возможен параметрический резонанс — маятник в виде груза массы М, подвешенного на нити, длину L которой можно изменять (рис. 1). Маятник с неподвижной точкой подвеса совершает собственные колебания с частотой
ω0=√g/L, причём сила натяжения нити (равная по величине сумме центробежной силы и составляющей силы тяжести, направленной вдоль нити) максимальна в нижнем положении груза и минимальна в крайних. Поэтому если уменьшать L в нижнем и увеличивать в крайних положениях, то работа внешней силы, совершаемая в среднем за период, оказывается положительной и колебания могут раскачиваться. На Параметрическом резонансе основано самораскачивание на качелях, когда эффективаня длина маятника периодически изменяется при приседаниях и вставаниях качающегося. Параметрический резонанс учитывается в небесной механике при расчёте возмущений планетных орбит, вызванных влиянием других планет.
Устройство маятника с переменной длиной L подвеса (а); схема движения тела маятника за один период (б)
Рис.1
В колебательных системах с нескольких степенями свободы (например, в системе из двух связанных контуров, маятников и др.) возможны нормальные колебания (моды) с различными частотами ω1, ω2. Поэтому колебания энергии, запасенной в каком-либо реактивном элементе, содержат не только составляющие с частотами 2ω1, 2ω2, но и с частотами, равными суммам и разностям различных нормальных частот. Соответственно нарастание колебаний здесь возможно как при выполнении условия (1) для любой из нормальных частот, так и, например, при изменении параметра с суммарной частотой:
ωн =ω1 + ω2 (1)
Параметрический резонанс приводит к самовозбуждению обоих нормальных колебаний с определенным соотношением фаз. Резонансная связь мод возможна также при ωн=ω1 - ω2, однако при этом вместо самовозбуждения происходит лишь периодическая перекачка энергии между модами. Соотношение (1) выражает закон сохранения энергии при распаде кванта «накачки» с энергией ћω на два кванта: ћω1 и ћω2. Отсюда следует также, что мощность Рн, поступающая в колебательную систему на частоте ωн, и мощности P1,P2 потребляемые на частотах ω1 и ω2, пропорциональны соответствующим частотам (частный случай т. н. соотношений Мэнли — Роу):
Pн/ωн=P1/ω1=P2/ω2


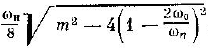 ,
,
![]() 1. "Основы теории колебаний" Мигулин В.В, Медведев В.И., Мустель Е.Р., Парыгин В.Н. - М.: Наука, 1978.
1. "Основы теории колебаний" Мигулин В.В, Медведев В.И., Мустель Е.Р., Парыгин В.Н. - М.: Наука, 1978.
![]() 2. "Автоколебательные системы" Теодорчик К.Ф. - М.: Гостехиздат, 1952.
2. "Автоколебательные системы" Теодорчик К.Ф. - М.: Гостехиздат, 1952.
![]() 3. "Введение в теорию колебаний" Стрелков С.П. - М.: Наука, 1964.
3. "Введение в теорию колебаний" Стрелков С.П. - М.: Наука, 1964.