|
|
 |
|
Межотраслевая Интернет-система поиска и синтеза физических принципов действия преобразователей энергии
|
Общий каталог эффектов
 | Свободные колебания маятника |
 |
Собственные (свободные) колебания маятника
Описание
Свободными колебаниями или собственными колебаниями называются колебания в механической, электрической или какой-либо другой физической системе, совершающиеся при отсутствии внешнего воздействия за счёт первоначально накопленной энергии (вследствие наличия начального смещения или начальной скорости). Характер свободных колебаний определяется главным образом собственными параметрами системы (массой, индуктивностью, ёмкостью, упругостью). В реальных системах вследствие рассеяния энергии свободные колебания всегда затухающие, а при больших потерях они становятся апериодическими. Время затухания колебаний определяется добротностью системы.
Маятником называют твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси. В физике под маятником обычно понимают маятник, совершающий колебания под действием силы тяжести (при этом его ось не должна проходить через центр тяжести тела) или силы упругости. При свободных колебаниях маятника происходит периодическое преобразование кинетической энергии маятника в потенциальную энергию силы тяготения или силы упругости пружины. Часто маятник обладает единственной собственной частотой колебаний.
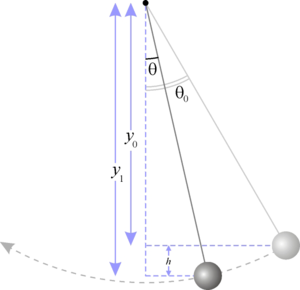
Рассмотрим колебания математического маятника. Математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести (рис.1).
Математический маятник
Рис.1
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
.png)
,
где ω ― частота собственных колебаний маятника, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах. Уравнение малых колебаний маятника около нижнего положения равнвесия (т.н. гармоническое уравнение) имеет вид:
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным дифференциальным уравнением второго порядка, для определения закона движения маятника необходимо задать два начальных условия - координату и скорость, из которых определяются две независимых константы:
x = Asin(θ0 + ωt),
где A - амплитуда колебаний маятника, θ
0 - начальная фаза колебаний, ω -
циклическая частота (
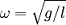
), которая определяется из уравнения движения. Движение, совершаемое маятником, называется
гармоническими колебаниями.
Ключевые слова
Разделы наук
Используется в научно-технических эффектах
Используется в областях техники и экономики
Используются в научно-технических эффектах совместно с данным эффектом естественнонаучные эффекты
Применение эффекта
В природе, и особенно в технике, чрезвычайно большую роль играют колебательные системы, т.е. те тела и устройства, которые сами по себе способны совершать периодические движения. “Сами по себе” - это значит не будучи принуждаемы к этому действием периодических внешних сил. Такие колебания называются поэтому свободными колебаниями в отличие от вынужденных, протекающих под действием периодически меняющихся внешних сил.
Всем колебательным системам присущ ряд общих свойств:
1. У каждой колебательной системы есть состояние устойчивого равновесия.
2. Если колебательную систему вывести из состояния устойчивого равновесия, то появляется сила, возвращающая систему в устойчивое положение.
3. Возвратившись в устойчивое состояние, колеблющееся тело не может сразу остановиться.
Реализации эффекта
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где sn - это синус Якоби, являющийся одной из эллиптических функций 2-го рода. Для
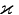
< 1 он является периодической функцией, при малых
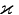
совпадает с обычным тригонометрическим синусом.
Параметр
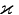
определяется выражением
,
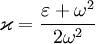
где
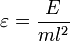
- энергия маятника в единицах t
-2.
Период колебаний нелинейного маятника
,
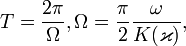
где K - эллиптический интеграл первого рода.
Колебательный контур — электрическая цепь, содержащая параллельно соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения). Колебательный контур - простейшая система в которой могут происходить свободные электромагнитные колебания.
Пусть конденсатор ёмкостью C заряжен до напряжения U0. Энергия, запасённая в конденсаторе составляет
EC =CU02/2.
При соединении конденсатора с катушкой индуктивности в цепи потечёт ток I, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия колебательного контура EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна EL = LI02/2, где L — индуктивность катушки, I0 — максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения − U0.
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
Напряжение, возникающее в катушке при изменении протекающего тока равно
.
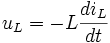
Аналогично для тока, вызванного изменением напряжения на конденсаторе:
.
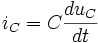
Поскольку всё возникающее в катушке напряжение падает на конденсаторе, то uL = uC, а ток, вызванный конденсатором проходит через катушку, то iC = iL. Дифференцируя одно из уравнений и подставляя результат в другое, получаем
.
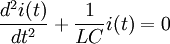
Это уравнение гармонического осциллятора с круговой частотой
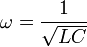
(иначе - собственной частотой гармонического осциллятора).
Литература
1. "Основы теории колебаний" Мигулин В.В, Медведев В.И., Мустель Е.Р., Парыгин В.Н. - М.: Наука, 1978.
2. "Автоколебательные системы" Теодорчик К.Ф. - М.: Гостехиздат, 1952.
3. "Введение в теорию колебаний" Стрелков С.П. - М.: Наука, 1964.
