|
|

 |
|
Межотраслевая Интернет-система поиска и синтеза физических принципов действия преобразователей энергии
|
Общий каталог эффектов
 | Уровни Ландау |
 |
Энергетические уровни для заряженной частицы в магнитном поле
Анимация
Описание
Уровни Ландау - энергетические уровни для заряженной частицы в магнитном поле. Впервые получены как решение уравнения Шрёдингера для заряженной частицы в магнитном поле Л. Д. Ландау в 1930 году. Решением этой задачи являются волновые функции электрона в гармоническом потенциале.
В классической механике движение частиц подчиняется второму закону Ньютона: ускорение равно силе, поделённой на массу, и направлено вдоль вектора силы. Сила, действующая на частицу в магнитном поле (сила Лоренца), пропорциональна произведению скорости движения частицы, напряжённости магнитного поля, заряду частицы, и синусу угла между направлением движения частицы и направлением магнитного поля. Направление силы перпендикулярно направлению магнитного поля и направлению движения частицы, и определяется правилом левой руки. Это правило можно проиллюстрировать простыми примерами:
* если частица движется вдоль магнитного поля, сила, действующая на неё, равна нулю
* если частица не заряжена, сила, действующая на неё, равна нулю
* если магнитного поля нет, сила, действующая на частицу, равна нулю
* если магнитное поле удвоить, сила, действующая на частицы, удвоится
* если скорость частицы увеличится в 10 раз (а направление движения останется тем же), сила, действующая на неё, тоже увеличится в 10 раз
* если частица движется поперёк магнитного поля, а другая, с тем же зарядом и с той же скоростью - под углом 30° к магнитному полю, сила, действующая на вторую частицу, в 2 раза меньше (потому что Sin 30° = 1/2) .
Заряженная частица в постоянном магнитном поле будет или вращаться по окружности в плоскости, перпендикулярной вектору индукции магнитного поля, или двигаться по спирали, причём ось спирали параллельна оси магнитного поля. Частица может иметь какую угодно энергию, и радиус окружности или спирали может быть каким угодно. Это было известно ещё в XIX веке.
В квантовой механике у частиц нет определённой координаты и можно говорить только о вероятности найти частицу в некоторой области пространства. Состояние частицы описывается волновой функцией, а динамика частицы (или системы частиц) описывается не вторым законом Ньютона, а гораздо более сложным уравнением Шредингера. (Уравнение Шредингера справедливо только в нерелятивистском случае, то есть когда скорости движения частиц значительно меньше скорости света, в противном случае действует ещё более сложное уравнение Дирака). Характерной особенностью уравнения Шредингера является то, что его собственные значения могут быть дискретны. Например, планеты могут вращаться вокруг Солнца на орбитах с любым радиусом и могут иметь непрерывный набор значений энергии, а электрон в атоме водорода в квазиклассическом приближении «обращается» вокруг протона на орбитах с определёнными радиусами и может обладать только некоторыми разрешенными энергиями, представленными в энергетическом спектре. С открытием законов квантовой механики, возник вопрос - а что происходит с движением частиц в магнитном поле в квантовомеханическом случае? Для решения этого вопроса необходимо решить уравнение Шредингера. Впервые это сделал 1930 году советский физик Ландау. Оказалось, что вдоль магнитного поля частица может двигаться с любой скоростью; но при заданной проекции скорости вдоль магнитного поля, частица может занимать дискретные энергетические уровни. Эти уровни были названы уровнями Ландау. Ниже приводится уравнение Шредингера и его решения.
Энергетический спектр для электрона (значение энергии в зависимости от его состояния) в магнитном поле в трёхмерном случае представляется в простом виде
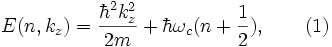
где ħ - постоянная Планка, ωc= eB/(mc) - циклотронная частота (СГС), B - внешнее магнитное поле, c - скорость света в вакууме, e - элементарный электрический заряд, m - масса электрона, kz - волновой вектор в направлении вектора z, которое принято за направление магнитного поля. Здесь энергетический спектр (1) легко интерпретировать. Движение вдоль магнитного поля, где магнитное поле не влияет на заряженную частицу, представлено плоскими волнами, как для свободной частицы с волновым вектором kz. Движение в направлении, перпендикулярном магнитному полю, ограничено, и энергетический спектр полностью квантован. Хотя движение частицы происходит в трёхмерном пространстве, энергетический спектр зависит только от двух квантовых чисел: непрерывного kz и дискретного n. Это означает, что спектр частицы является вырожденным. В трёхмерном случае наблюдается двухкратное вырождение энергии по проекции волнового вектора на направление магнитного поля ±kz. В дополнение к этому имеется вырождение уровня Ландау, равное
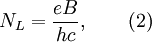
где h — постоянная Планка. Кратность вырождения каждого из уровней Ландау равна отношению площади сечения образца плоскостью, перпендикулярной магнитному полю, к площади круга с радиусом равным магнитной длине
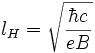
, что является характерным размером области высокой вероятности нахождения частицы.
Кроме того, для свободных электронов в трёхмерном пространстве наблюдается приблизительное двукратное вырождение уровней энергии по спину. Это вырождение, однако, нетривиально, поскольку для него требуется, чтобы уровень Ландау для электрона со спином вниз в точности совпадал с уровнем Ландау для электрона со спином вверх плюс магнитный момент электрона на магнитное поле. Другими словами, требуется, чтобы g-фактор для электрона был в точности равен двойке (это, как учит квантовая электродинамика, не совсем так). Это требование тем более не выполняется для электронов — квазичастиц в твёрдых телах (эффективная масса электрона и его магнитный момент мало связаны). Тем не менее, задача об электроне со спином и g-фактором равным 2 представляет некоторый теоретический интерес, поскольку её можно представить как задачу, обладающую суперсимметрией.
Ключевые слова
Разделы наук
Используется в научно-технических эффектах
Используется в областях техники и экономики
Используются в научно-технических эффектах совместно с данным эффектом естественнонаучные эффекты
Применение эффекта
С открытием законов квантовой механики, возник вопрос – а что происходит с движением частиц в магнитном поле в квантово-механическом случае? Для решения этого вопроса необходимо решить уравнение Шредингера. Впервые это сделал 1930 году советский физик Ландау. Оказалось, что вдоль магнитного поля частица может двигаться с любой скоростью; но при заданной проекции скорости вдоль магнитного поля, частица может занимать дискретные энергетические уровни. Эти уровни были названы уровнями Ландау.
Существованием уровней Ландау объясняется диамагнетизм электронов проводимости в металлах и полупроводниках. Этот эффект иначе известен как диамагнетизи Ландау.
Учет уровней Ландау важен при рассмотрении систем заряженных частиц в магнитном поле в различных задачах физики плазмы, физики твердого тела (например, в эффекте де Хааза - ван Альфена, квантовании лифшица-Онзагера), астрофизики.
Уровни Ландау играют существенную роль во всех кинетических явлениях в присутствии магнитного поля.
Реализации эффекта
Стационарное уравнение Шрёдингера для электрона в магнитном поле представлено в виде
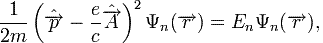
(1)
где
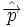
и
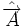
— оператор импульса электрона и векторный потенциал магнитного поля соответственно,
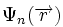
— волновая функция электрона,
En — энергия и индекс
n обозначает
n-ый уровень Ландау. В калибровке Ландау уравнение (1) запишется в виде
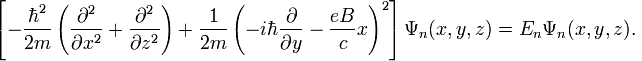
(2)
Чтобы разделить переменные в этом уравнении, решение удобно искать в виде произведения трёх функций
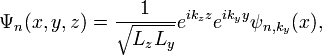
(3)
где Lz и Ly — размеры системы, kz и ky — волновые векторы, индекс ky у волновой функции ψn,ky(x) означает, что она зависит от него как от параметра. Подставляя (3) в (2) получим одномерное уравнение для ψn,ky(x)
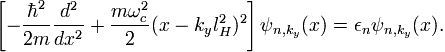
(4)
Это уравнение — не что иное, как уравнение Шрёдингера для гармонического осциллятора со сдвигом минимума потенциала. Таким образом, решения запишутся в виде
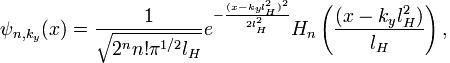
(5)
где Hn(x) — полином Эрмита порядка n.
Рассмотрим влияние электрического поля на энергетический спектр электрона в магнитном поле. Перепишем уравнение
с учётом электрического поля ε, направленного по x
которое после выделения полного квадрата представляется в виде
где
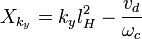
и
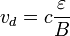
. Мы видим из гамильтониана, что электрическое поле просто сдвигает центр волновой функции. Энергетический спектр задаётся следующим выражением:
Литература
 1. Физическая энциклопедия / Гл. ред. А.М. Прохоров. Ред. кол.: Д.М. Алексеев, А.М. Балдин, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др.– М.: Большая Российская энциклопедия. Т.2
1. Физическая энциклопедия / Гл. ред. А.М. Прохоров. Ред. кол.: Д.М. Алексеев, А.М. Балдин, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др.– М.: Большая Российская энциклопедия. Т.2
 2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 тт: Т. 3: Квантовая механика: Нерелятивистская теория: Учебное пособие для вузов (под ред. Питаевского Л.П.) Изд. 6-е, испр. М: Физматлит, 2004
2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 тт: Т. 3: Квантовая механика: Нерелятивистская теория: Учебное пособие для вузов (под ред. Питаевского Л.П.) Изд. 6-е, испр. М: Физматлит, 2004


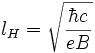 , что является характерным размером области высокой вероятности нахождения частицы.
, что является характерным размером области высокой вероятности нахождения частицы.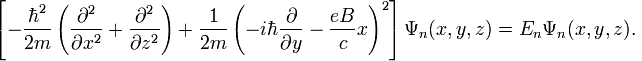 (2)
(2)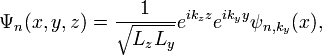 (3)
(3)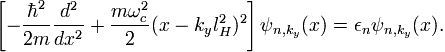 (4)
(4)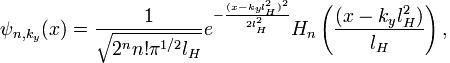 (5)
(5)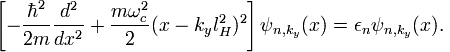
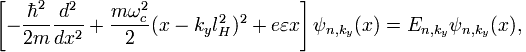
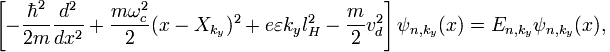
![]() 1. Физическая энциклопедия / Гл. ред. А.М. Прохоров. Ред. кол.: Д.М. Алексеев, А.М. Балдин, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др.– М.: Большая Российская энциклопедия. Т.2
1. Физическая энциклопедия / Гл. ред. А.М. Прохоров. Ред. кол.: Д.М. Алексеев, А.М. Балдин, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др.– М.: Большая Российская энциклопедия. Т.2
![]() 2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 тт: Т. 3: Квантовая механика: Нерелятивистская теория: Учебное пособие для вузов (под ред. Питаевского Л.П.) Изд. 6-е, испр. М: Физматлит, 2004
2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: В 10 тт: Т. 3: Квантовая механика: Нерелятивистская теория: Учебное пособие для вузов (под ред. Питаевского Л.П.) Изд. 6-е, испр. М: Физматлит, 2004