|
|

 |
|
Межотраслевая Интернет-система поиска и синтеза физических принципов действия преобразователей энергии
|
Общий каталог эффектов
 | Устойчивость движения |
 |
Способность механических систем слабо менять свое состояние или свойства под действием возмущений
Описание
Устойчивость движения —способность систем слабо менять (в том или ином смысле) своё состояние или свойства под действием возмущений. Теория устойчивости —это совокупность представлений и методов, обобщающих и формализующих различные аспекты устойчивости разнообразных систем. Наиболее распространёнными понятиями теории устойчивости являются устойчивость по Ляпунову, орбитальная устойчивость, асимптотическая устойчивость, структурная устойчивость.
Пусть траектория L динамической системы задаётся отображением x(t)=Ttx0, где х—совокупность координат точки в фазовом пространстве системы, Тt — оператор эволюции, преобразующий начальное состояние системы с координатами х0 в состояние с координатами x(t) в момент времени t. Траектория L устойчива по Ляпунову, если для сколь угодно малого ε можно найти такое δ, что для любого начального состояния х’0, близкого к х0, то есть ρ(х0,x’0)< δ , всегда окажется ρ (Тt х0, Тt x’0) < ε .Здесь ρ(x1,x2) — расстояние между точками x1 и х2 в фазовом пространстве. Если
То устойчивость называется асимптотической, а если к тому же
То устойчивость называется экспоненциальной.
Пусть L — некоторая траектория системы, а Uε(L) — некоторая её ε - окрестность то есть ρ(x,L)< ε для любой точки x принадлежащей Uε(L); здесь и ниже ρ(x,L) — расстояние от точки x до множества L в фазовом пространстве. Если для любого ε можно найти такое δ, что всякая траектория, начинающаяся в Uδ(L), всегда остаётся в Uε(L), то траектория L называется орбитально (орбитно) устойчивой. Если к тому же существует такое δ0, что при всех δ < δ0 для любой траектории {x(t)}, начинающейся в Uδ(L),
то траектория называется асимптотически орбитально устойчивой.
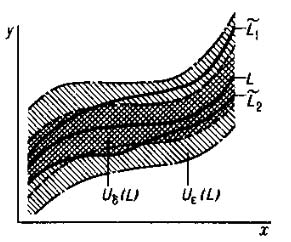
Геометрический смысл орбитальной устойчивости
рис.1
Геометрический смысл орбитальной устойчивости проиллюстрирован на рис.1 (L—исходная, L1 и L2 —возмущённые траектории на фазовой плоскости {х, у}). Для устойчивости по Ляпунову требуется также малость расстояния между одновременными точками на близких траекториях (в указанном выше смысле). Из устойчивости по Ляпунову следует устойчивость орбитальная. Обратное, вообще говоря, не верно: две траектории могут быть сколь угодно близкими, а расстояние между двумя одновременными точками на них может расти и стать немалым, даже если в начальный момент эти точки близки. Например , для уравнения Дуффинга:
с начальными условиями
все траектории периодические. Период решения τ растёт от 2πω до бесконечности по мере роста амплитуды А от нуля до А0. При достаточно малых изменениях начальных условий траектории системы оказываются близкими. Однако благодаря зависимости периода решения от амплитуды близкие в начальный момент точки на двух соседних траекториях со временем разойдутся на большое расстояние. Поэтому при любых а>0 фазовые траектории системы устойчивы орбитально и неустойчивы по Ляпунову. В пределе а = 0 уравнение переходит в уравнение гармонических колебаний, период которых не зависит от амплитуды τ = 2π/ω, и все траектории оказываются устойчивыми по Ляпунову.
Если в уравнении гармонических колебаний учтено трение
то такая система имеет асимптотически (экспоненциально) устойчивую траекторию.
Асимптотически устойчивое множество траекторий L в фазовом пространстве динамической системы называется аттрактором, если оно: 1) компактно и неразложимо на отдельные структурные элементы; 2) инвариантно относительно Тt: TtL=L 3) оператор Тt рекуррентен на L, то есть для сколь угодно больших времён t0>0 траектория у(t)=Тtх произвольной точки x при t>t0 пройдёт в сколь угодно малой окрестности точки х. В случае замкнутых траекторий последнее требование означает бесконечнократное прохождение системой каждой точки траектории, то есть периодическое движение (в силу теоремы Коши). Примеры аттракторов: асимптотически устойчивые стационарные состояния; устойчивые предельные циклы: странные аттракторы (отвечающие стохастическим колебаниям в нелинейных диссипативных системах).
Если автономная динамическая система
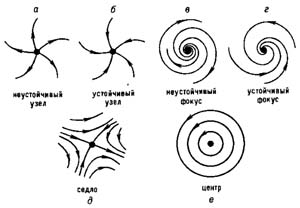
имеет двумерное фазовое пространство, х = {x1, х2} , то ее состояния равновесия х=хс определяются из системы уравнений f(х) = 0. На фазовой плоскости {x1, х2} поведение траекторий в окрестности одного из состояний равновесия может иметь вид, показанный на рис. 3: состояния равновесия (а, в, д) — неустойчивые, (б, г)— асимптотически устойчивые, равновесие (е)—устойчивое, но не асимптотически.
Поведение траекторий в окрестности точки равновесия
рис.3
Если размерность фазового пространства больше чем 2, то наряду с указанными типами устойчивости могут появляться и более сложные, комбинирированные типы (например, седло — узел, узел—фокус).
Ключевые слова
Разделы наук
Применение эффекта
Теория устойчивости — многообразная дисциплина, изучающая закономерности поведения систем под действием внешних воздействий. Система называется устойчивой, если малые изменения внешних воздействий вызывают малые изменения поведения системы. Наибольшее развитие получила теория устойчивости механических систем. Действительно, именно механика как старейшая наука, впервые столкнулась с проблемами устойчивости. Эйлер впервые строго поставил и решил задачу устойчивости состояния равновесия механический системы - стержня, сжатого сжимающей силой.
Устойчивость движения - одно из важнейших понятий механики. Движение любой механической системы, например машины, гироскопического устройства, самолёта, снаряда, зависит от действующих сил и начальных условий, то есть от положений и скоростей точек системы в момент начала движения. Зная эти силы и начальные условия, можно теоретически рассчитать, как будет двигаться система.
Теория устойчивости движения имеет важное практическое значение для многих областей техники, так как устойчивостью движения должны обладать различного рода двигатели, автомобили, самолёты, ракеты, гироскопические приборы, системы автоматического регулирования. В небесной механике проблема устойчивости возникает при изучении вопроса о длительности сохранения структуры солнечной системы, двойных звёзд.
Реализации эффекта
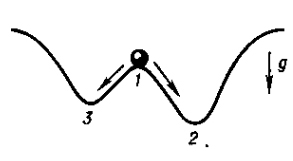
Наглядным примером, демонстрирующим некоторые аспекты понятия устойчивости, является простейшая динамическая система; тяжёлый шарик на неровной поверхности (рис.1):в точке 1 потенциальная энергия шарика имеет максимум, и это положение равновесия неустойчиво: под действием малых возмущений шарик скатывается в более низкую точку (2 или 3), где его потенциальная энергия имеет минимум.
Тяжелый шарик на неровной поверхности
рис.1
Если пренебречь трением, то шарик будет в течение бесконечного времени совершать колебания вблизи положения устойчивого равновесия (точек 2 и 3). Если шарик начнёт скатываться с точки, более низкой, чем точка 1, то амплитуда колебаний будет меньшей (так как начальная энергия системы меньше). Однако близким начальным данным будут отвечать траектории с близкими периодами и амплитудами (орбитальная устойчивочть). В том случае, когда трение не мало, скорость шарика будет убывать и он остановится в точке устойчивого равновесия. Это состояние устойчиво асимптотически, в фазовом пространстве является притягивающим множеством. Если слабо деформировать поверхность, то характер движения не изменится (структурная устойчивость).
В качестве примера рассмотрим гироскоп (волчок), ось которого вертикальна и который вращается вокруг этой оси с угловой скоростью ω. Теоретически ось гироскопа должна оставаться вертикальной при любом значении ω, но фактически, когда ω меньше некоторой величины ωкр, ось при любом малом возмущении (толчке) будет всё более отклоняться от вертикали. Если же ω больше ωкр, то малые возмущения практически направление оси не изменят. Следовательно, при ω<ωкр гироскоп по отношению к направлению его оси неустойчив, а при ω>ωкр устойчив. Последнее неравенство и является критерием устойчивости, при этом
где Р вес гироскопа, а расстояние от точки опоры до центра тяжести , Ix и Iy – моменты инерции гироскопа относительно осей х и у соответственно.
Литература
 1. Прохоров А.М. Физическая энциклопедия. М.: Большая Российская энциклопедия, 1998
1. Прохоров А.М. Физическая энциклопедия. М.: Большая Российская энциклопедия, 1998
 2. Ляпунов А.М. Общая задача об устойчивости движения. Л.; М., 1950
2. Ляпунов А.М. Общая задача об устойчивости движения. Л.; М., 1950
 3. Четаев Н.Г. Устойчивость движения. М., 1990
3. Четаев Н.Г. Устойчивость движения. М., 1990


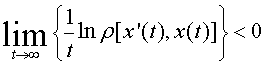
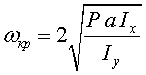
![]() 1. Прохоров А.М. Физическая энциклопедия. М.: Большая Российская энциклопедия, 1998
1. Прохоров А.М. Физическая энциклопедия. М.: Большая Российская энциклопедия, 1998
![]() 2. Ляпунов А.М. Общая задача об устойчивости движения. Л.; М., 1950
2. Ляпунов А.М. Общая задача об устойчивости движения. Л.; М., 1950
![]() 3. Четаев Н.Г. Устойчивость движения. М., 1990
3. Четаев Н.Г. Устойчивость движения. М., 1990